티스토리 뷰
1. 컴퓨터의 자료표현
▶ 컴퓨터에서의 자료표현
1) 컴퓨터에서의 자료표현
- 2진수 코드 : (1,0) (True/False), (on/off)
- 최소단위 : 비트(bit)
- 4비트그룹 : 니블(Nibble)
- 8비트그룹 : 바이트(Byte)
- 2) n비트로 2 n개의 상태를 표시
▶ 컴퓨터 내부에서 표현할 수 있는 자료의 종류
- 수치자료, 문자자료, 논리자료, 포인터자료, 문자열자료
- 1과 0의 조합인 2진수로 표현

2. 수치/진수 자료 표현
▶ 10진수의 표현
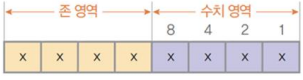
1) 존(Zone)형식의 표현
10진수 한 자리를 표현하기 위해서 1바이트(8비트)를 사용하는 형식
① 존 영역 : 상위 4비트, 1111로 표현
② 수치 영역 : 하위 4비트, 표현하고자 하는 10진수 한 자리 값에 대한 2진수 값을 표시
- 표현 순서 : 2의 3제곱=8 -> 2의 2제곱=4 -> 2의 1제곱=2 -> 2의 0제곱=1
2) 여러 자리의 10진수 표현방법
① 10진수의 자릿수만큼 존 형식을 연결하여 사용
② 마지막 자리의 존 영역에 부호를 표시 양수(+) : 1100 음수(-) : 1101

3) 팩(Pack) 형식의 표현
① 존 영역 없이 4비트를 사용하여 10진수 한자리수 표현
② 최하위 4비트에 부호를 표시 양수(+) : 1100 음수(-) : 1101

▶ 2진수의 정수 표현
1) 2진수의 정수 표현
① 일정한 길이의 n비트로 표현, 부호와 절댓값 형식으로 표현
- MSB값을 바꿔 음수를 간단히 표현할 수 있음.
- 가산기와 감산기가 모두 필요하므로 하드웨어 구성비용이 많이 듦.
- +0(00000000)과 -0(10000000)이 존재하므로 논리적으로 맞지 않음.
- n비트로 (2 n-1 -1)~+(2 n-1 -1)의 범위를 표현할 수 있음.
② 최상위 1비트 : 부호 (양수(+) : 0, 음수(-) : 1)
③ 나머지 n-1 비트 : 이진수 표시

2) 1의 보수(Complement) 형식
- n비트를 모두 1로 만든 이진수에서 변환하고자 하는 이진수를 뺌
- (A-B)뺄셈을 (A+(B의 1의 보수))로 변환하여 계산할 수 있으므로, 가산기 회로로 감산을 수행할 수 있음.
- +0(00000000)과 -0(11111111)이 존재하므로 논리적으로 맞지 않음.
- n비트로 (2 n-1 -1)~+(2 n-1 -1)의 범위를 표현할 수 있음.
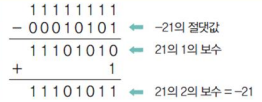
3) 2의 보수(Complement) 형식
- 1의 보수에 1을 더해서 표현
- (A-B)뺄셈을 (A+(B의 2의 보수))로 변환하여 계산할 수 있으므로 가산기 회로로 감산을 수행가능.
- 덧셈 연산에서 발생하는 오버플로 처리가 1의 보수 형식보다 간단함.
- 컴퓨터 시스템에서 실제로 사용하는 형식.
- n비트로 2 n-1 ~+(2 n-1 -1)의 범위를 표현할 수 있음.
▶ 2진수의 실수 표현
1) 2진수의 실수 표현
- 실수 : 정수부와 소수부 사이에 소수점이 있는 숫자
- 컴퓨터는 2진수만으로 실수 표현하기에 소수점을 직접 표현하지 못하고 정수부와 실수부의 위치로 실수를 표현
① 고정 소수점 표현
- 소수점이 항상 최상위 비트의 왼쪽 밖에 고정되어 있는 것으로 취급하는 방법
- 고정 소수점 표현의 00010101은 0.00010101의 실수 값을 의미
② 부동 소수점 형식의 표현
- 고정 소수점 형식에 비해서 표현 가능한 값의 범위가 넓음.
- 실수를 구분하여 표현
- 부호, 지수부, 가수부 구분
- a는 4바이트(32비트) 단정도 방식, b는 8바이트(64비트) 배정도 방식
- 부호 : 양수 0, 음수 1

v C로 배우는 쉬운 자료구조, 이지영, 한빛아카데미
'자료구조' 카테고리의 다른 글
| 자바 자료구조 | 1-3. 알고리즘과 시간 복잡도 (0) | 2022.05.31 |
|---|---|
| 자바 자료구조 | 1-2. 컴퓨터가 데이터를 다루는 방법 (0) | 2022.05.30 |
| 자바 자료구조 | 1. 개요 (0) | 2022.05.30 |
| 🌞[자료구조] 자료 표현 - 문자, 논리, 포인터, 문자열 자료 (0) | 2022.01.07 |
| 🌞[자료구조] 자료구조의 개념과 분류, SW코딩이란? (0) | 2022.01.05 |
- Total
- Today
- Yesterday
- 2019 카카오 개발자 겨울 인턴십
- ASCII코드
- 자료구조
- 2진수
- 카카오 코딩테스트
- 프로그래머스 # 음양더하기
- 백준
- Git
- java
- 1063
- 프로그래머스
- 자료표현
- 알고리즘
- 오
- 인형뽑기
- 10진수
- 구현
- 브루트포스
- solved.ac
- 크레인 인형뽑기 게임
- K번째수
- stack
- 코딩테스트
- 킹
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
